
The letter ‘c’ in complementary comes before the letter ‘s’ in supplementary, just like 90° comes before 180°.Hence when two supplementary angles are put together they form a ‘straight’ angle. The letter‘s’ for ‘supplementary’ and‘s’ for ‘straight’.Hence when two complementary angles put together to form a ‘corner right’ angle. The letter ‘c’ for ‘complementary’ and ‘c’ for ‘corner’.Then, by the definition of supplementary angles,Ĭomplementary vs Supplementary Angles Complementary AnglesĮach participating angle is complement of the otherĮach participating angle is supplement of the other A pair of angles are said to be complementary if their sum is 90 degrees.

Let ∠POB is supplementary to ∠AOP and ∠QOB A pair of angles are said to be supplementary if their sum is 180 degrees.

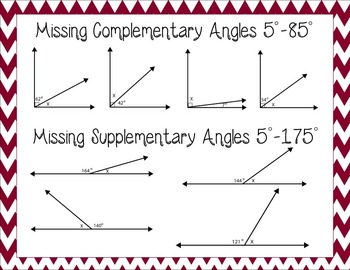
Exclusions Students will not cover vertically opposite angles. Prerequisites Students should already be familiar with identifying right and straight angles, adding the measures of adjacent angles. Equate the sum of these measures with 90° or 180° and solve for the value of x. If they are adjacent they will form a straight angle. find the measure of an angle given its supplementary angle, solve word problems using complementary and supplementary angles. The measure of another angle in the pair is represented as a linear expression. Similar to complementary angles, the two angles do not need to be adjacent. The word ‘supplementary’ came from the Latin word ‘supplere’ meaning ‘supply’. Each angle in the pair is said to be the supplement of the other. Two angles are called supplementary angles if the sum of their measure equals 180°. A staircase that have an escalation of 30° and the wall at 90°.Hands of a clock showing 3PM and the seconds hand pointing towards the digit 2.The sum of two complementary angles is 90. So, three angles can never be supplementary, even though the sum of their angles is 180 degrees or 90 degrees. Complementary and supplementary angles are always in pairs. When a rectangular piece of bread is divided into two pieces by cutting along the diagonal, we get two right triangles, each with a pair of complementary angles. The sum of supplementary angles is 180 degrees, so when we place them adjacent to each other, they form a straight angle.Hence Proved Real Life Examples of Complementary Angles In other words when you add the measure of one angle in. Then, by the definition of complementary angles, Supplementary and Complementary Angles Supplementary angles are two angles whose sum is equal to 180. They can either be adjacent or non-adjacent. Why? Because the sum of the angles in a triangle equals 180°, and by subtracting the right angle, we're left with 90° for the two remaining angles.ĭealing with the trigonometric functions of two angles may be pretty tough, unless you know a relationship between them.Let ∠ZOW is complementary to ∠XOZ and ∠YOW The complementary and supplementary angles are those that add up to 90 degrees and 180 degrees respectively. Well, just think about a right triangle again - the two acute angles of such a triangle are complementary. There are analogical situations for any other shape that has a right angle.Īnd what is an example of some non-adjacent complementary angles? Take a look at a right triangle's height - did you notice that altitude, h c, from the right angle to the hypotenuse creates two similar triangles? The adjacent complementary angles have also the same measures as the angles in the original right triangle.Angle Bisector: A ray (or line or segment) that divides an. The same works for a special type of rectangle - a square - here the angle and its complementary angle are even equal to each other (45°). Can you think of a way to remember the difference between complementary and supplementary angles 3. Look at the diagonal of the rectangle: it splits the right angle into two adjacent complementary angles.When learning geometry, you will often find adjacent complementary angles, even though you don't notice or pay much attention to them!


 0 kommentar(er)
0 kommentar(er)
